
Adição de Monômios:
Regras:
1º passo: identificar os termos semelhantes.
2º passo: somar ou subtrair os coeficientes dos termos semelhantes.
3º passo: conservar a parte literal.
4º passo: simplificar a expressão e colocar a resposta correta.
EX 1: 5ab + 3b - 5a + a - 2b - 3ab=
5ab - 3ab + 3b - 2b - 5a + a=
2ab + b - 4a
EX 2: 3x³y² - 2xy + x³y² - 3xy + 4xy - x³y²=
3x³y ²+ x³y² -x³y² - 2xy -3xy +4xy=
3x³y² - xy
Multiplicação de Monômios:
Regras:
1º passo: multiplicar os coeficientes.
2º passo: conservar a parte literal e somar os expoentes ou juntar as variáveis que são diferentes.
EX 1: 3x²y . 5xy=
15x³y²
EX 2: 2m - 5n . 1/3p=
10/3mnp
Potência de Monômios:
Regras:
1º passo: elevar o coeficiente numérico à potência dada na questão.
2º passo: multiplicar os expoentes das variáveis com o expoente das variáveis com o expoente da questão ( o expoente que está fora dos parenteses ).
3º passo: escrever corretamente o resultado obtido.
EX 1:
 Raiz quadrada de um monômio:
Regras:
1º passo
Raiz quadrada de um monômio:
Regras:
1º passo: calcular a raiz quadrada do coeficiente numérico.
2º passo: dividir por "2" o expoente de cada variável.
3º passo: escrever corretamente o resultado dado.
EX 1:
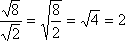






 :
:
.jpg)

![\sqrt[n]{a}](http://upload.wikimedia.org/wikipedia/pt/math/9/a/2/9a2b6d33f3d62a1e8bd99c76f3cb79f5.png) representa o único número real x que verifica
representa o único número real x que verifica  e tem o mesmo sinal que a (quando existe). Quando n é omitido, significa que n=2 e o símbolo de radical refere-se à
e tem o mesmo sinal que a (quando existe). Quando n é omitido, significa que n=2 e o símbolo de radical refere-se à  radical.
radical.

.jpg)


 Todo número natural e todo número inteiro vai ser um número racional, ou seja,
Todo número natural e todo número inteiro vai ser um número racional, ou seja,


